A Note on compact hypersurfaces in a Euclidean space - 22/11/12
| pages | 4 |
| Iconographies | 0 |
| Vidéos | 0 |
| Autres | 0 |
Abstract |
In this Note, we show that the presence of a unit Killing vector field ξ on an orientable compact hypersurface of a Euclidean space with shape operator A and induced metric g such that is a constant, renders it to be a round sphere and also influences the dimension of the ambient Euclidean space.
Résumé |
Supposons la donnée dʼun champs de vecteurs unitaire de Killing ξ sur une hypersurface compacte, orientable, dʼun espace euclidien, avec opérateur de forme A et métrique induite tels que soit constant. Nous montrons dans cette Note que cela impose que lʼhypersurface est nécessairement isométrique à une sphère de courbure constante et que lʼespace euclidien ambiant est de dimension paire.
Plan
| ☆ | This Work is supported by King Saud University, Deanship of Scientific Research, Research Group Project No. RGP-VPP-182. |
Vol 350 - N° 21-22
P. 971-974 - novembre 2012 Retour au numéroBienvenue sur EM-consulte, la référence des professionnels de santé.
L’accès au texte intégral de cet article nécessite un abonnement.
Bienvenue sur EM-consulte, la référence des professionnels de santé.
L’achat d’article à l’unité est indisponible à l’heure actuelle.
Déjà abonné à cette revue ?



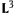 containing a light-like line
containing a light-like line