An extreme variation phenomenon for some nonlinear elliptic problems with boundary blow-up - 14/02/08


| pages | 6 |
| Iconographies | 0 |
| Vidéos | 0 |
| Autres | 0 |
Abstract |
Let
 be a smooth bounded domain in
be a smooth bounded domain in
and
be a non-empty open and closed subset of
![]()
 . Denote by
. Denote by either the Dirichlet or the mixed boundary operator on
when
. We consider the nonlinear elliptic problem
in
 , subject to
, subject to on
when
, where a is a real number, b is a continuous non-negative function on
, while
is continuous on
such that
is increasing on
. Assuming that f varies rapidly at infinity with index
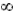 (i.e.,
(i.e., for all
), we establish the uniqueness of the positive solution satisfying
on
and describe its blow-up rate via the extreme value theory. To cite this article: F.-C. Cîrstea, C. R. Acad. Sci. Paris, Ser. I 339 (2004).
Résumé |
Soit
 un domaine borné, régulier de
un domaine borné, régulier de
et
un sous-ensemble ouvert et fermé de
![]()
 . On désigne par
. On désigne par ou bien une condition de Dirichlet ou bien une condition mixte sur
si
. On étudie le problème elliptique non-linéaire
dans
 , avec la condition
, avec la condition sur
si
, où a est un réel, b est une fonction continue non-négative dans
et
est continue sur
telle que
est strictement croissante sur
. Supposons que f varie rapidement à lʼinfini dʼindex
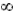 (i.e.,
(i.e., pour tout
), on établit alors lʼunicité de la solution positive avec
sur
et on décrit le taux dʼexplosion au bord en utilisant la théorie des valeurs extrêmes. Pour citer cet article : F.-C. Cîrstea, C. R. Acad. Sci. Paris, Ser. I 339 (2004).
Plan
Vol 339 - N° 10
P. 689-694 - novembre 2004 Retour au numéroBienvenue sur EM-consulte, la référence des professionnels de santé.
L’accès au texte intégral de cet article nécessite un abonnement.
Bienvenue sur EM-consulte, la référence des professionnels de santé.
L’achat d’article à l’unité est indisponible à l’heure actuelle.
Déjà abonné à cette revue ?

