Sieving and expanders - 15/02/08
| pages | 5 |
| Iconographies | 0 |
| Vidéos | 0 |
| Autres | 0 |
Abstract |
Let V be an orbit in of a finitely generated subgroup
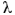 of
of whose Zariski closure
is suitably large (e.g. isomorphic to
). We develop a Brun combinatorial sieve for estimating the number of points on V for which a fixed set of integral polynomials take prime or almost prime values. A crucial role is played by the expansion property of the congruence graphs' that we associate with V. This expansion property is established when
. To cite this article: J. Bourgain et al., C. R. Acad. Sci. Paris, Ser. I 343 (2006).
Résumé |
Soit V lʼorbite dans dʼun sous-groupe finiment engendré de
donʼt lʼadhérence dans la topologie de Zariski est suffisament grande (p.e. est isomorphe à
). Nous developpons une crible combinatoire de Brun a fin dʼestimer le nombre de points de V pour lesquels un system de polynômes donnés prennent des valeurs premières ou presque premières. Des propriétés dʼexpansion de certain « graphes de congruence » y jouent un rôle crucial, quʼon établi dans le cas
. Pour citer cet article : J. Bourgain et al., C. R. Acad. Sci. Paris, Ser. I 343 (2006).
Plan
Vol 343 - N° 3
P. 155-159 - août 2006 Retour au numéroBienvenue sur EM-consulte, la référence des professionnels de santé.
L’accès au texte intégral de cet article nécessite un abonnement.
Bienvenue sur EM-consulte, la référence des professionnels de santé.
L’achat d’article à l’unité est indisponible à l’heure actuelle.
Déjà abonné à cette revue ?


